Rumus Herron (Luas segitiga sebarang jika diketahui panjang ketiga sisinya)

Segitiga adalah bangun datar yang mempunyai 3 sisi dan 3 sudut pada bagian dalamnya. Symbol untuk segitiga adalah Δ. Segitiga diberi nama dengan menggunakan 3 huruf pada ketiga titik sudutnya.

Mempelajari konsep segitiga sangatlah penting untuk mempelajari bentuk-bentuk lain yang lebih kompleks (bangun ruang).
Jenis segitiga
Berdasarkan sisinya dibedakan menjadi:

1. Segitiga sama sisi; segititga dengan tiga sisi yang berukuran sama panjang.
2. Segitiga sama kaki: segitiga dengan dua sisi berukuran sama panjang.
3. Segitiga sembarang: segitiga yang memiliki tiga sisi dengan ukuran yang berbeda.

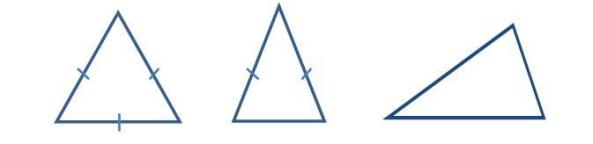
Berdasarkan sudutnya segitiga dikelompokan sebagai berikut:

1. Segitiga siku-siku: segitiga yang mempunyai satu sudut siku-siku didalamnya.
2. Segitiga tumpul: segitiga yang mempunyai sudut tumpul (lebih besar dari 90° tetapi kurang dari 180°) pada bagian dalamnya.
3. Segitiga lancip: segitiga yang semua sudut dalamnya lancip (kurang dari 90°).

Alas dan Tinggi

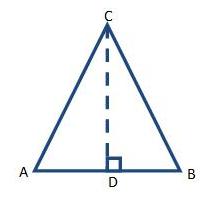
Setiap segitiga mempunyai tiga alas (setiap sisinya) dan tiga garis tinggi. Garis tinggi adalah ruas garis tegak lurus dari suatu sudut ke sisi yang berlawanan.
Dari gambar diatas dapat diambil contoh tinggi dari salah satu tinggi dari segitiga tersebut adalah CD dengan alas AB.


Konsep Luas Segitiga

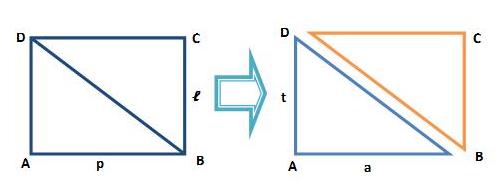
Jika persegi panjang tersebut dibagi menjadi dua menurut diagonalnya, maka terbentuk dua buah segitiga. maka Luas segitiga adalah L = 1/2 x p x ℓ
Dalam segitiga p = a (alas) dan l = t (tinggi).
Dalam mencari luas segitiga bisa juga dicari dari bangun datar yang lain, misalnya jajar genjang.
PEMBUKTIAN RUMUS SEGITIGA L= √(s (s-a )(s-b)(s-c))
Buktikan bahwa rumus luas ∆ABC jika ukuran ketiga sisinya diketahui, yaitu a, b, c adalah

L= √(s (s-a )(s-b)(s-c))

dengan s adalah ½ keliling segitiga tersebut atau s = ½ (a + b + c)
PEMBUKTIAN
sin² A + cos² A = 1
sin² A = 1 – cos² A
sin² A = (1 + cos A) (1 – cos A )
Ingat aturan cosinus:

Ingat bahwa s = ½ (a + b + c), maka
1. (a + b + c) = 2s
2. (b + c + a) = (a + b + c) – 2a = 2s – 2a = 2 (s – a )
3. (a + b – c) = (a + b + c) – 2c = 2s – 2c = 2 (s –c )
4. (a + c – b) = (a + c + b) – 2b = 2s – 2b = 2 (s –b )
Sehingga,
Ingat bahwa luas segitiga adalah:

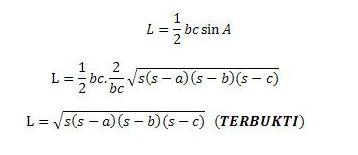
Konsep keliling segitiga
Keliling segitiga dapat dicari dengan rumus :

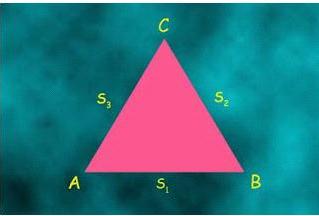
K = S₁ + S₂ + S₃
Ket :
K = Keliling
S₁ = Sisi pertama
S₂ = sisi kedua
S₃ = sisi ketiga
Referensi:
http://aimprof08.wordpress.com/2012/08/21/pembuktian-rumus-luas-segitiga/
http://forum.indowebster.com/showthread.php?t=138719
http://www.proprofs.com/quiz-school/story.php?title=segitiga-keliling-luas-segitiga-rumadi

Posted in: